浅谈js中浮点数精度问题及解决方法
背景
最近项目中,有涉及到金额的计算以及相关的运算判断,由于忽略了浮点数存在的问题,导致一些判断和计算在某些情况下出现问题,导致bug产生。虽说之前已了解浮点型计算相关问题,但没有在实际的开发过程中重视,加之之前很少接触到金额相关数字处理的业务场景,导致,重蹈前人之覆辙。在此,做一个记录和简单刨析,以加深印象。
问题
0.1 + 0.2 // 输出:0.30000000000000004
4.56 * 100 // 输出:455.99999999999994
4.56 - 2.56 // 输出:1.9999999999999996
如以上代码所示,某些情况下,运算出的值和预期不符,这就是浮点数的精度问题。所以,在处理数字相关运算的时候,如果忽略了这个问题,必然会导致某些情况下bug的出现。对于涉及到钱的问题上,这个问题还是马虎不得的。为什么会出现这样的问题呢?
原因
浮点和浮点数
在计算机科学中,浮点(英语:floating point,缩写为FP)是一种对于实数的近似值数值表现法,由一个有效数字(即尾数)加上幂数来表示,通常是乘以某个基数的整数次指数得到。以这种表示法表示的数值,称为浮点数(floating-point number)。利用浮点进行运算,称为浮点计算,这种运算通常伴随着因为无法精确表示而进行的近似或舍入。
以上的定义,引用自维基百科:浮点数。浮点数即是一种对实数的近似表示法,“近似”这两个字就是我们计算不准确的根本原因。
二进制和十进制的转换
计算机内部是使用二进位制的运算,在计算之前会将我们使用的十进制数值,转换为二进制数值,然后再进行运算。我们可以通过除2取余法,来将十进制数值,转换为二进制数值。然后从后往前依次排列对应的数字即得到二进制对应的数值,我们可以用一个简单的方法描述这个过程:
// 6/2 = 3 余 0
// 3/2 = 1 余 1
// 1/2 = 0 余 1
// 则结果即为 110
/**
* 十进制整数转二进制
* @param {Number} decimal
* @return {Number} 二进制数据
*/
function decimalToBinary(decimal) {
if (isNaN(decimal)) {
console.warn('input value must be Number');
return decimal;
}
// 是否为整数
if (!Number.isInteger(decimal)) {
console.warn('input value must be Int');
return decimal;
}
let num = Number(decimal);
let numArr = [];
// 不断循环取余数推入数组
while (num >= 1) {
if (num === 1) {
numArr.unshift(1);
break;
}
numArr.unshift(num % 2);
num = Math.floor(num / 2);
}
return Number(numArr.join(''));
}
decimalToBinary(2) // 10 <= 2^2 + 0
decimalToBinary(3) // 11 <= 2^2 +2^1
decimalToBinary(4) // 100 <= 2^3
decimalToBinary(5) // 101 <= 2^3 + 2^0
二进制转换为十进制比较简单,可通过2的次幂累加得到,比如二进制11,转为为十进制为 2^1+2^0 = 3。对于整数,进行二进制和十进制的转换还是比较简单的。但是对于小数就稍微复杂一点。十进制小数转换为二进制小数可通过乘2取整法进行换算,将小数,一直乘以2,将结果个位数取出取出,再拿小数去乘2,依次进行。小数的二进制转十进制方法和整数类似,取2的次幂即可。文字描述不好理解,下面通过示例进行描述:
// eg: 0.625和0.1为例
/*
*** 0.625 ***
* 0.625 * 2 = 1.25 取出 1 继续拿剩下的0.25计算
* 0.25 * 2 = 0.5 取 0 剩余0.5
* 0.5 * 2 = 1 取 1 剩余 0
* 0 * 2 = 0 …… ……
* 则最后的到结果为 0.10100000... 即为0.101
转换为十进制相当于 2^-1 + 0^-2 + 2^-3 = 1/2 + 0 + 1/8 = 0.625
*/
/*
*** 0.1 ***
* 0.1 * 2 = 0.2 取出 0 剩下的0.2计算
* 0.2 * 2 = 0.4 取 0 剩余0.4
* 0.4 * 2 = 0.8 取 0 剩余 0.8
* 0.8 * 2 = 1.6 取 1 剩余 0.6
* 0.6 * 2 = 1.2 取 1 剩余 0.2 这里将开始和第一行一样,进入循环了
* 0.2 * 2 = 0.4 取 0 剩余 0.4
* 0.4 * 2 = 0.8 取 0 剩余 0.8
* ...此时已经进入了无线循环了 0011
* 则最后的到结果为 0.0 0011 0011 0011 0011 0011……
* 转换为10进制相当于 2^-4 + 2^-5 + 2^-8 +2^-9 …… 1/16 + 1/32 +。。。。。
* 可以看出二进制描述的十进制其实是2的次幂的无限逼近,所以最终就导致了误差存在
*/
从以上的二进制小数转换为十进制小数过程中,0.625刚好可以很好的用二进制0.101表示,但是,0.1却不行。对于像0.1这类数,实际上二进制是通过无限去逼近这个数字,却不能完全等于,所以就出现了误差,当位数取得越小,误差越大。0.1即1/10,小于1/23(即八分之),大于1/24,所以只能用一个最解决1/10的2的N次幂去累加,这时就产生了误差。
javascript精度
在 JavaScript 中, Number 是一种 定义为 64位双精度浮点型(double-precision 64-bit floating point format) (IEEE 754)的数字数据类型。在其他编程语言中,有不同的数字类型存在,比如:整型(Integers),单精度浮点型(Floats),双精度浮点型(Doubles),大数(Bignums)。
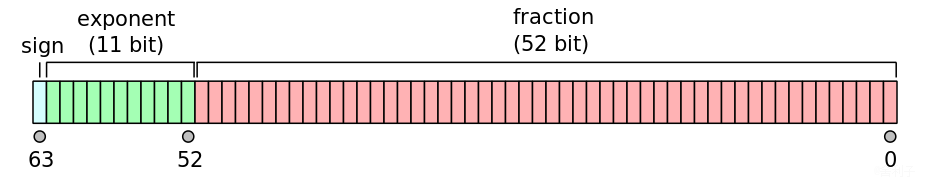
上图为64位双精度浮点表示,其中第1位为sign位,用来正负类型。2-12共11位用来表示次方数,剩余的52位表示精确度。IEEE 754 标准的 64 位双精度浮点数的小数部分最多支持53位二进制位,能表示的十进制小数在15~17位之间。2^−53 ≈ 1.11 × 10^−16。正是由于这个精度问题,就导致了根本的问题。
通过上面转换2进制小数的方法,我们分别可以计算得出二进制的0.1和0.2,分别为
0.0001100110011001...
0.0011001100110011...
然后相加计算,因精度问题,要截断52位之后结果为:0.0100110011001100110011001100110011001100110011001100 ,然后,转换为10进制即为:0.30000000000000004。
解决方法
由上面的问题可以看出,其实,我们所要解决的就是误差问题。对此我们可以先将小数转换为整数,然后将其四舍五入,再将其除回去即即可满足要求,下面提供一种简单的处理方法,由于是临时写的,可能存在纰漏未考虑到情况,如需使用,请先测试,代码如下:
/**
* 获取小数中小数点后的位数
* @param {Number} num 传入的小数
* @returns {Number} 小数点后的位数
*/
function getDecimalLen(num) {
if (isNaN(num)) {
return;
}
// 判断是否是小数 不是小数返回0
if (Number.isInteger(num)) {
return 0;
}
const len = num.toString().split('.')[1].length;
return len;
}
/**
* 对数字进行四舍五入
* @param {Number} num 传入的数字
*/
function numRound(num) {
if(num >= 0) {
return Math.round(num);
}
// 解决round负数处理的问题
return -Math.round(-num);
}
/**
* 对两个数进行运算返回处理后的值,解决精度导致的问题
* @param {Number} first 需要运算的第一位数值
* @param {String} type 运算的类型 取值未 + - * /
* @param {Number} second 需要运算的第一位数值
* @return {Number} 运算后的结果
*/
function computedFloatNumber(first, type, second) {
// 分别获取参与运算两个数字的小数位数
const maxLen = Math.max(getDecimalLen(first), getDecimalLen(second));
// 取最大得位数对应的10得次方分别与两个数相乘,将小数转换为整数
const baseNum = Math.pow(10, maxLen);
// 将其进行四舍五入进一步解决精度问题
const firstVal = numRound(first * baseNum);
const secondVal = numRound(second * baseNum);
const comput = {
'+': (firstVal + secondVal) / baseNum,
'-': (firstVal - secondVal) / baseNum,
'*': (firstVal * secondVal) / Math.pow(baseNum, 2),
'/': (firstVal / secondVal)
};
return comput[type] || 0;
}
以上思路即先将小数转换为整数,然后进行四舍五入解决精度问题,再除以对应的乘数还原小数。这里注意,乘法要出乘数的平方。
